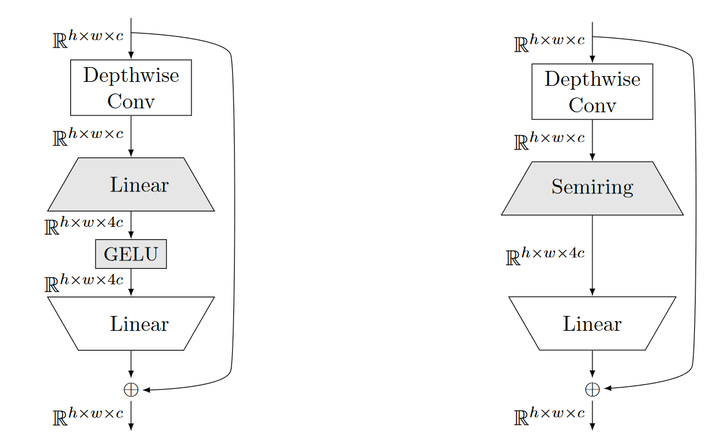
 ConvNeXt architecture with standard activation functions versus semiring-based trainable non-linearities.
ConvNeXt architecture with standard activation functions versus semiring-based trainable non-linearities.
Abstract
We introduce a class of trainable nonlinear operators based on semirings that are suitable for use in neural networks. These operators generalize the traditional alternation of linear operators with activation functions in neural networks. Semirings are algebraic structures that describe a generalised notation of linearity, greatly expanding the range of trainable operators that can be included in neural networks. In fact, max- or min-pooling operations are convolutions in the tropical semiring with a fixed kernel. We perform experiments where we replace the activation functions for trainable semiring- based operators to show that these are viable operations to include in fully connected as well as convolutional neural networks (ConvNeXt). We discuss some of the challenges of replacing traditional activation functions with trainable semiring activations and the trade-offs of doing so.