 Smoothing of DW-MRI data using geometric flows.
Smoothing of DW-MRI data using geometric flows.
Abstract
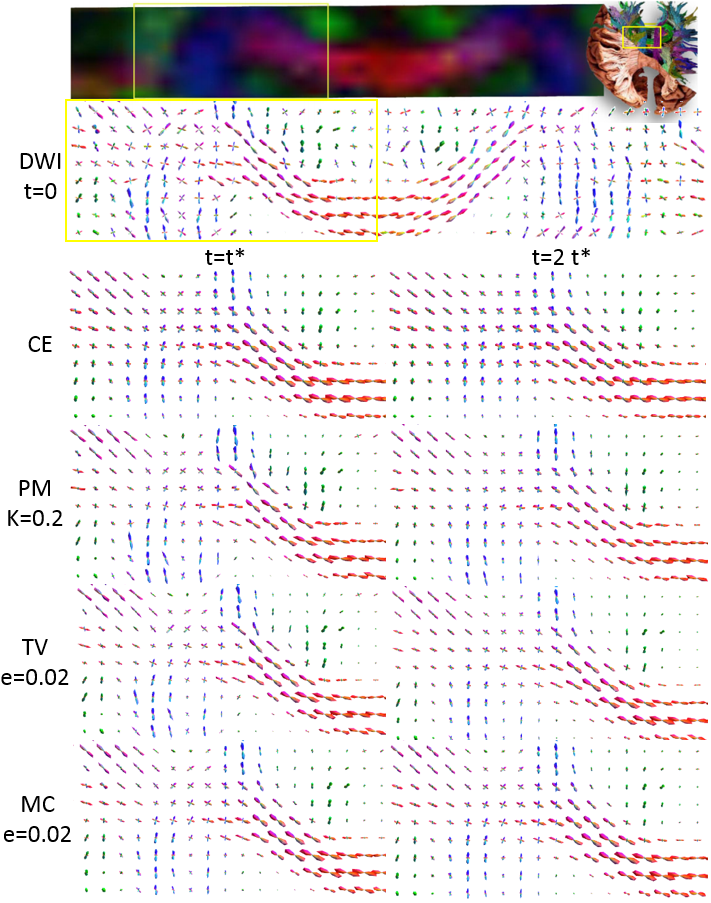
Total variation regularization and total variation flows (TVF) have been widely applied for image enhancement and denoising. To include a generic preservation of crossing curvilinear structures in TVF we lift images to the homogeneous space $M = \mathbb{R}^d \rtimes S^{d−1}$ of positions and orientations as a Lie group quotient in $SE(d)$. For $d = 2$ this is called ‘total roto-translation variation’ by Chambolle & Pock. We extend this to $d = 3$, by a PDE-approach with a limiting procedure for which we prove convergence. We also include a Mean Curvature Flow (MCF) in our PDE model on M. This was first proposed for $d = 2$ by Citti et al. and we extend this to $d = 3$. Furthermore, for $d = 2$ we take advantage of locally optimal differential frames in invertible orientation scores (OS). We apply our TVF and MCF in the denoising/enhancement of crossing fiber bundles in DW-MRI. In comparison to data-driven diffusions, we see a better preservation of bundle boundaries and angular sharpness in fiber orientation densities at crossings. We support this by error comparisons on a noisy DW-MRI phantom. We also apply our TVF and MCF in enhancement of crossing elongated structures in 2D images via OS, and compare the results to nonlinear diffusions (CED-OS) via OS.
An extended version of this paper was written for the JMIV special issue following SSVM 2019.