Geodesic Tracking via New Data-driven Connections of Cartan Type for Vascular Tree Tracking
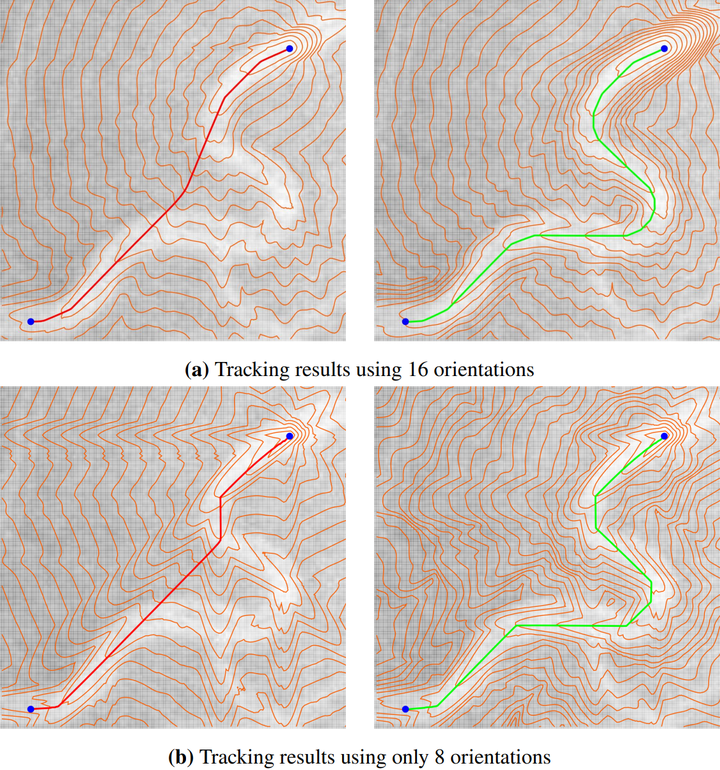 Using gauge frames allows us to reduce the number of orientations in our lifted image and still retain superior tracking.
Using gauge frames allows us to reduce the number of orientations in our lifted image and still retain superior tracking.
Abstract
We introduce a data-driven version of the plus Cartan connection on the 3D homogeneous space $\mathbb{M}_2$ of 2D positions and orientations. We formulate a theorem that describes all shortest and straight curves (parallel velocity and parallel momentum respectively) with respect to this new data-driven connection and corresponding Riemannian manifold. Then we use these shortest curves for geodesic tracking of complex vasculature in multi-orientation image representations defined on $\mathbb{M}_2$. The data-driven Cartan connection characterizes the Hamiltonian flow of all geodesics. It also allows for improved adaptation to curvature and misalignment of (lifted) vessel structure that we track via globally optimal geodesics. We compute these geodesics numerically via steepest descent on distance maps on $\mathbb{M}_2$ that we compute by a new modified anisotropic fast-marching method. Our experiments range from tracking single blood vessels with fixed endpoints to tracking complete vascular trees in retinal images. Single vessel tracking is performed in a single run in the multi-orientation image representation, where we project the resulting geodesics back onto the underlying image. The complete vascular tree tracking requires only two runs and avoids prior segmentation, placement of extra anchor points, and dynamic switching between geodesic models. Altogether we provide a geodesic tracking method using a single, flexible, transparent, data-driven geodesic model providing globally optimal curves which correctly follow highly complex vascular structures in retinal images.